
(自作の電気回路)
どうも、白滝です。
電気力線。
私はダイキライです。
あなたも、嫌いになってください。
だってね、
電気力線のせいで、ホントは体系的な電磁気学がゴチャゴチャになってるからです。
わかる?
わかってました?
本当の電磁気はもーっとわかりやすい。
ちょいちょいと勉強すれば、問題が解けるはずの教科なんです。
それを、電気力線はぶっ壊した。
この怒りを、あなたはわかりますでしょうか?
たぶんね、あなたが電磁気ができない1番の理由って「電気力線」じゃありません?
電気力線で、つまづいてる。
電気力線で、他の用語が意味わからんくなってる。
だってさ、
電気力線なんて、電磁気のプロフェッショナルが聞いてやっと理解できる代物だからだわ
ちゃんと全部学んで、よく理解したひとが使うもの。
まさかの学んで1発目に使うものではないんだな
わかりやすいけど、本質を真っ暗に覆ってしまう
電気力線のせいで、本質が見えないのです。
体系的ルールを外れた理<ことわり>が電気力線。
簡単に言えば、電磁気学のオマケです。
電気力線って、めっちゃ特殊な解き方だから。
知らなくても、問題は解ける。
そういった類の、チートツールでしょう。
それが前面に押し出されて、
ほかの大事な「電磁気学」が隠れてしまっている。
あれ、特殊な解き方です。
電磁気学が一通り頭に入っている人が、問題を簡単に解くために使うのが電気力線なのよ
ね?
知ってました?
あれです、こいつです、数学で言えば。
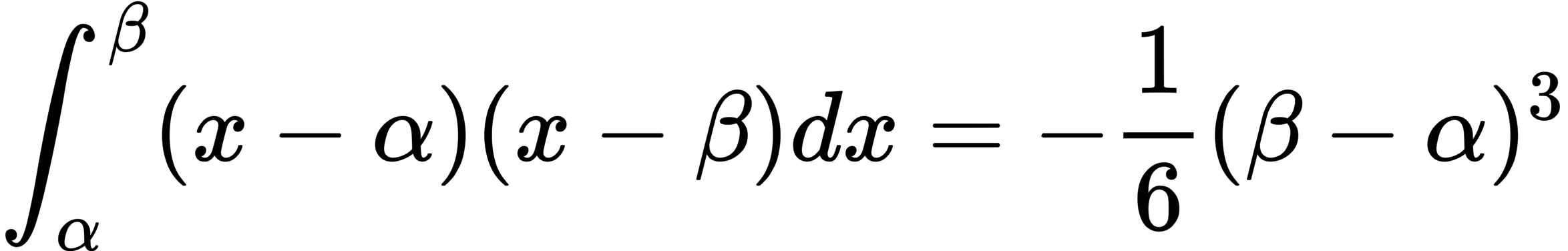
わかります?
このチートツール臭がプンプンしてる。
わかりやすくしてくれる代わりに、
積分の本質が見えないのがこの公式ですよねw
電気力線も同じ。ただのチートツールです。
わかった上で使うなら、いいけど。
電気力線は、高度な代物。
今までの単位とは、まったく別の考え方で生まれたオ・マ・ケが電気力線なんです。
オマケ。
知らなくても、問題は解けます。
電気力線そのものの使い方を問う問題以外なら、知らなくて大丈夫。
なのに、高校物理では真っ先に習うんです。
パッと見分かりやすいから。
説明しやすいから。
そんな理由で教えられたら、たまったもんじゃないんですけど。
電気力線は、目に見えない電気の力を「本数で数えたい!」という欲から生まれた
ああ、欲深い。
だから、電磁気学がこうも複雑になったのに。
ああ、電束と電気力線は違います。
(ここからフクザツ)
目に見えない電気の力は電束(電荷量)Qでも表したんですが、
電荷量Qをもつ=電束Qが出せる、つまり、電束(→)をQだけ出す能力がある物体という意味。
で、
電束は「量」なのです。
本数じゃない。
電束は矢印の本数ではなく「量」で、空間中の電気的な力を測っている。
そこでね、どっかの誰かが
電気の力を矢印の本数で表したい!
と言い出したんですよ。
もうね
善意だったとは思うんですが。
これで、フクザツになったのさ。
その人は、
「電束(電荷量)Q」を「その空間の誘電率ε」で割った値を「電気力線の本数 [本]」
としたのです。
電気力線の本数[本] = 電束(電荷量)Q[C] / その空間の誘電率ε[F/m]
ですね。
こう定義した。
こう定義したことで、空間中の電気的な力を「矢印の本数」で表せるようになったんですが、、
じゃあ、電気力線って結局なんなの!?
って話ですよね。
電束と同じようで、少し違う。
わけわからん用語(定義)が、生まれてしまったわけです。
じゃあ、電気力線とは?
説明しよう!
元から電荷量=電束(電荷を持った物体からは、目に見えない線が出ているという考え方)という考え方はあったが、本数ではなく数値の大小でしか見れなかったのだ!
だから、本数で数えたい!という声が多数に!電気力線が生まれたのだ
もう少し詳しくいうと、
電気力線とは
「電荷量Q=電束(→)をQだけ出す能力がある」って説明がわかりづらいから、Qをεで割って「電気力線がQ/ε本出ている」と説明したもの。
ですね。
電荷量Qをもつ=電束(→)をQ[C]だけ出す能力がある

電荷量Qをもつ=電気力線がQ/ε[本]出ている
うーん。
わかりやすくなってしまった。
この説明のしやすさだけのための定義。
それが、
電気力線の本数[本] = 電束(電荷量)Q[C] / その空間の誘電率ε[F/m]
なんですわ。
磁気力線は存在しないぜ!
そんでね、わかりづらいことに「磁気力線」はありません。
磁気は磁束の「量」で測ってください。
本数で測るシステムはありません。
ははっ
紛らわしいなあ。
おまけ。
磁束と磁気量に使う記号なんですが、(単位は同じ)
磁束にΦ[Wb]を使い、磁気量にm[Wb]と記号を使い分けている。
空間中の磁束を表す時はΦを使い、物体がもつ磁束を出す能力(磁気量)を表す時にはmを使う。
みたいです。
お役に立てば。
それでは!


