【前回の続き☆】
キラーンっ
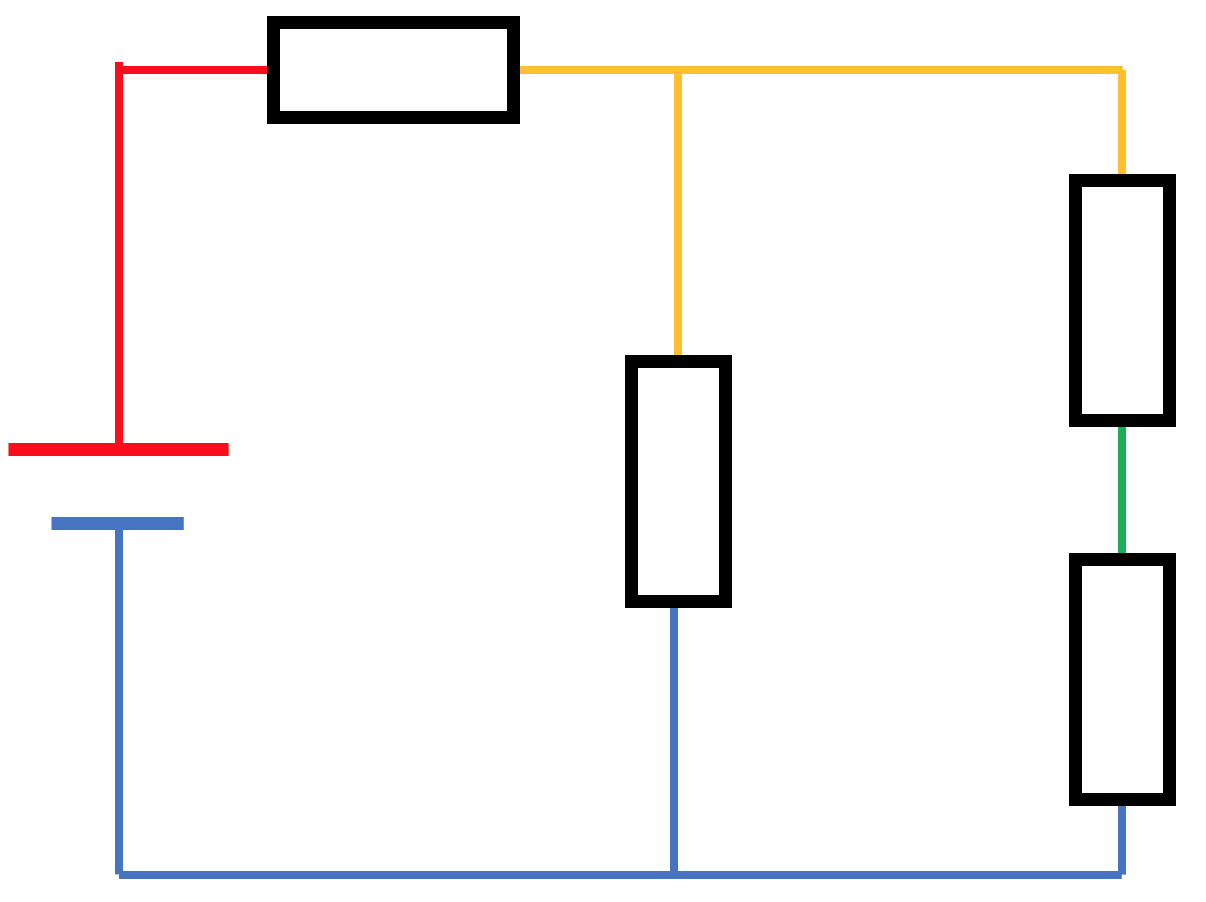
さて。
導線のカラーリングができたら、
次は各電位を追っていきますぜ?
※電位ってなにかって?電位=(電子の)電気的な位置エネルギーですよ・・・
はい。
■電位は「電子の」電気的な位置エネルギーのこと
■「同じ導線内の電子」の電位は同じ→導線はどこも電位が同じ
■導線の電位=電子の電位
ボナペティ♪♪
電位の復習です。
ちゃーんと
導線の中に電子のつぶつぶが見えますか?
で、その電子が
電気的なエネルギー(電位)を持っている
と知ってますか?
(導線は「電位をもっている電子が集まっている」から、電位を持つのです)
ね?
ここまで、おさらい。
デーンチは作るーよ、電位差(エネルギー差)を
(元ネタ⬆️)
いやはや
これもおさらいですね。
電池とは?

エネルギー差を作るもの。
これが、本質です。
電池を見たら、
あっ!エネルギー差を作る装置だっ!!
と思いましょう。
たとえばね、、

ご存知の通り、
15Vの電池(電源)は、15Vのエネルギー差(電位差)を作る
んだなあ・・・
電流を流すとか、流さないとか
の話ではないのです。
電池(電源)とは、
ただただ、「エネルギー差(電位差)」を作るだけの装置
なのね。
だから、
15V電源があったら、とりあえずこう書き込む。

これで、2色の電位がわかりましたね。
赤:15V
青:0V
(もう少し細かいこというとね、青は勝手に「0V」としたんだ。なぜかって?位置エネルギーはね、自分で基準「0V」をおくのよ)
のこりは2色。
入試問題って、
この電位を探す作業を問題にしてるんですよ?
黄色と青の電位は?
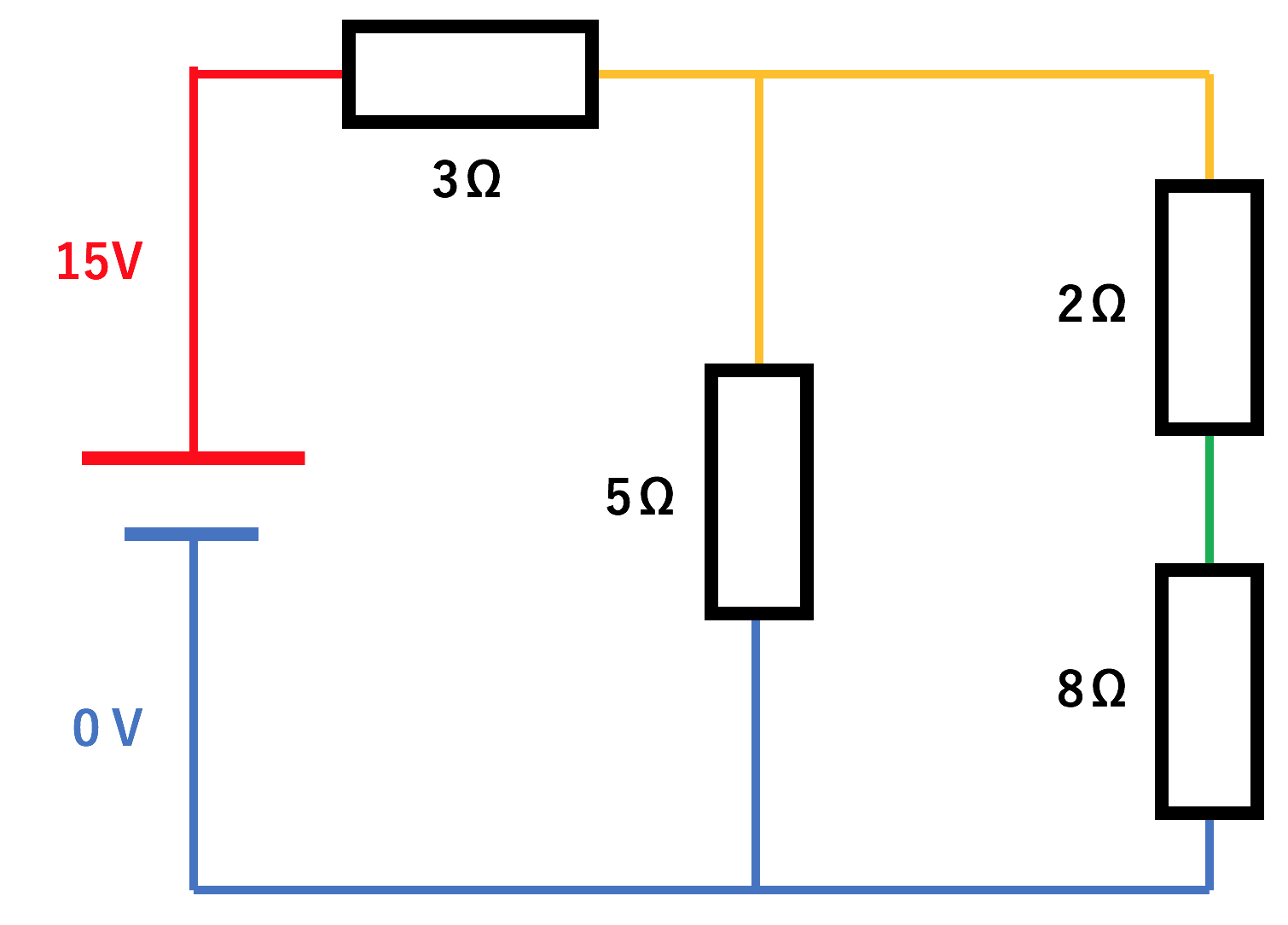
まあ、テキトーに抵抗値をおいてみました。
でぇ、デンッ!!
【問題】
この時、黄色と緑の電位はいくらになるでしょう?
って話になるよね。
どうする!?
抵抗の合成でも、しちゃう!?w
笑
高校生は、そんなことしません。ww
(難しい問題になると、解けなくなるやつww)
わかる人はね、
抵抗に電位差があると
電流が流れる
という本質を使います。
え、あたりまえ!?
まあ、そうです
本質とは、あたりまえのことなのです。
わかります?
直列:$R_0=R_1+R_2$
並列:$\frac{1}{R_0}=\frac{1}{R_1}+\frac{1}{R_2}$
とかいう
思考停止のチートツールじゃなくて・・・
当たり前の大前提
から答えを導いていく。
これが、大学入試の電気回路。
大学教授が求める解き方なんですわなー
わかるかなーw
だから、
あれです、あれ。
当たり前を使って、解いてみると・・・

さて。
抵抗に電位差があると
電流が流れる
って知識だけで、解けてしまいます。
(というか、これで解けないと中卒レベルww)
↓
↓
↓
抵抗に電位差があると
電流が流れるから・・・
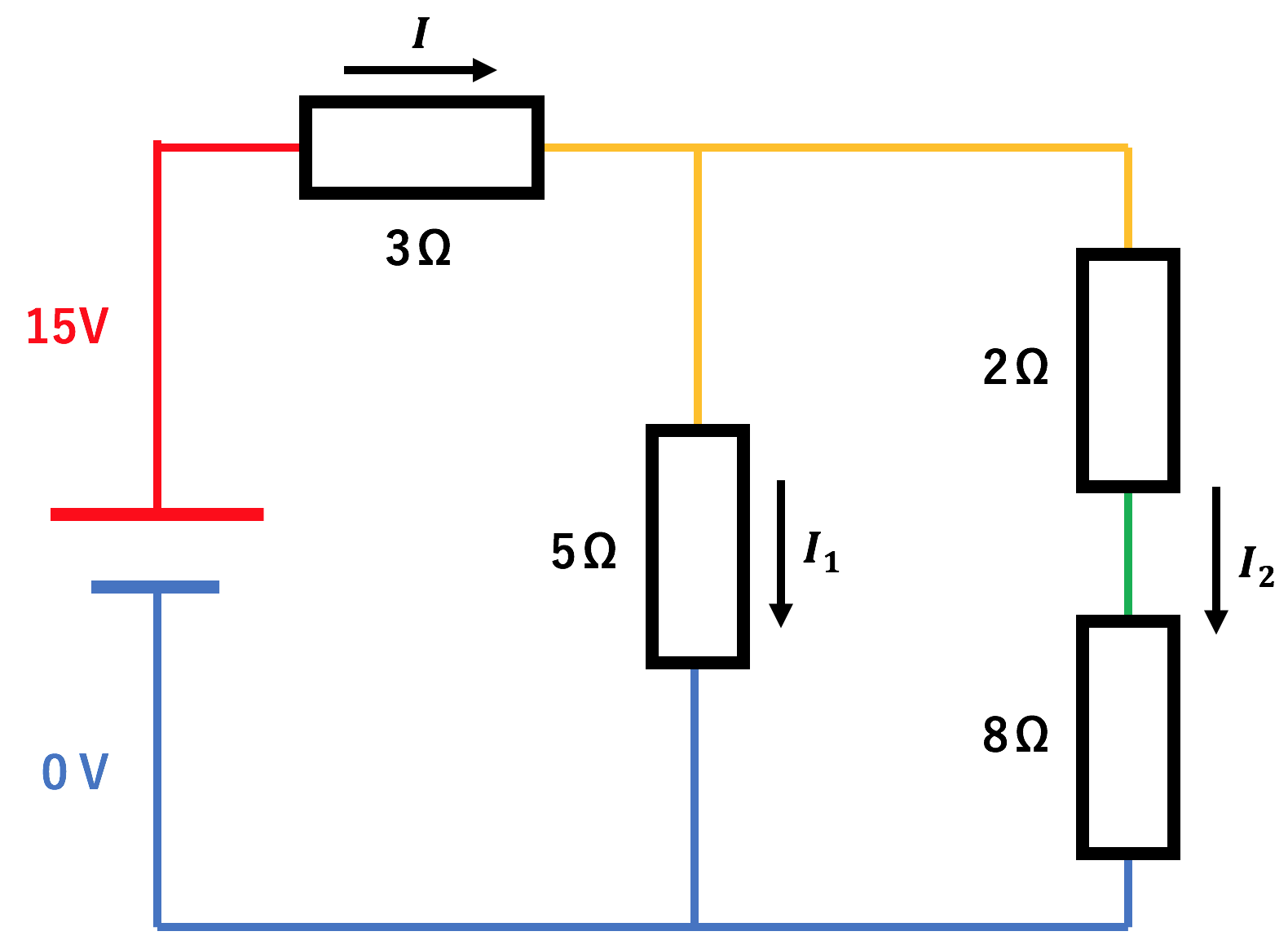
そう、
わからないものは文字で置く
という算数の超基本ですね。
なので、
わからない電位も文字で置いてしまいましょうか。
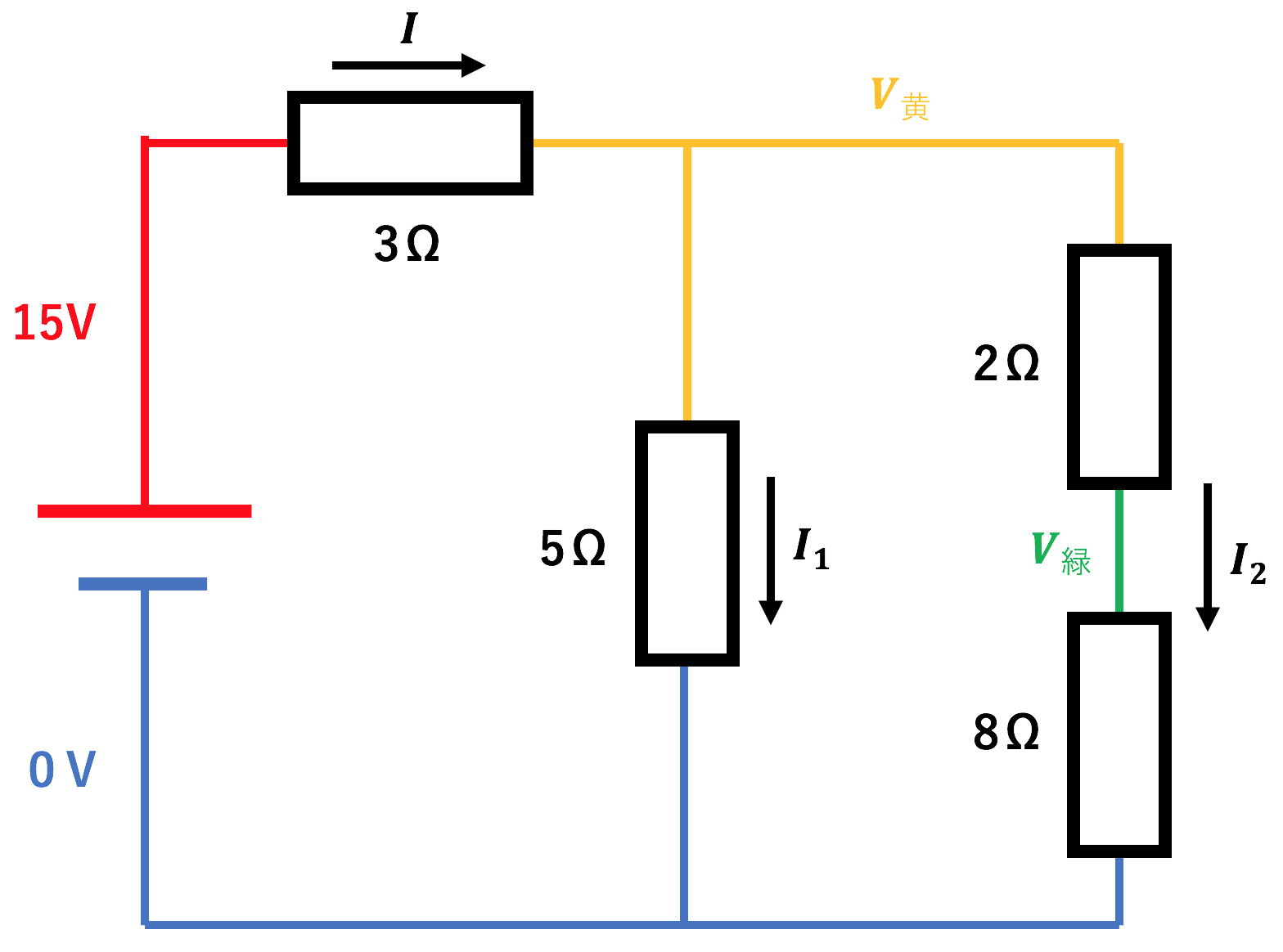
はい。
これで、
各部分個別で式を立てられるようになりましたっ!!
全体でなく、部分で
最初にいった標語みたいなやつ。
各抵抗で$V=RI$を立ててあげれば、
ただの算数に変わるのです
おわかり?
こういうことよ?
【①〜④】
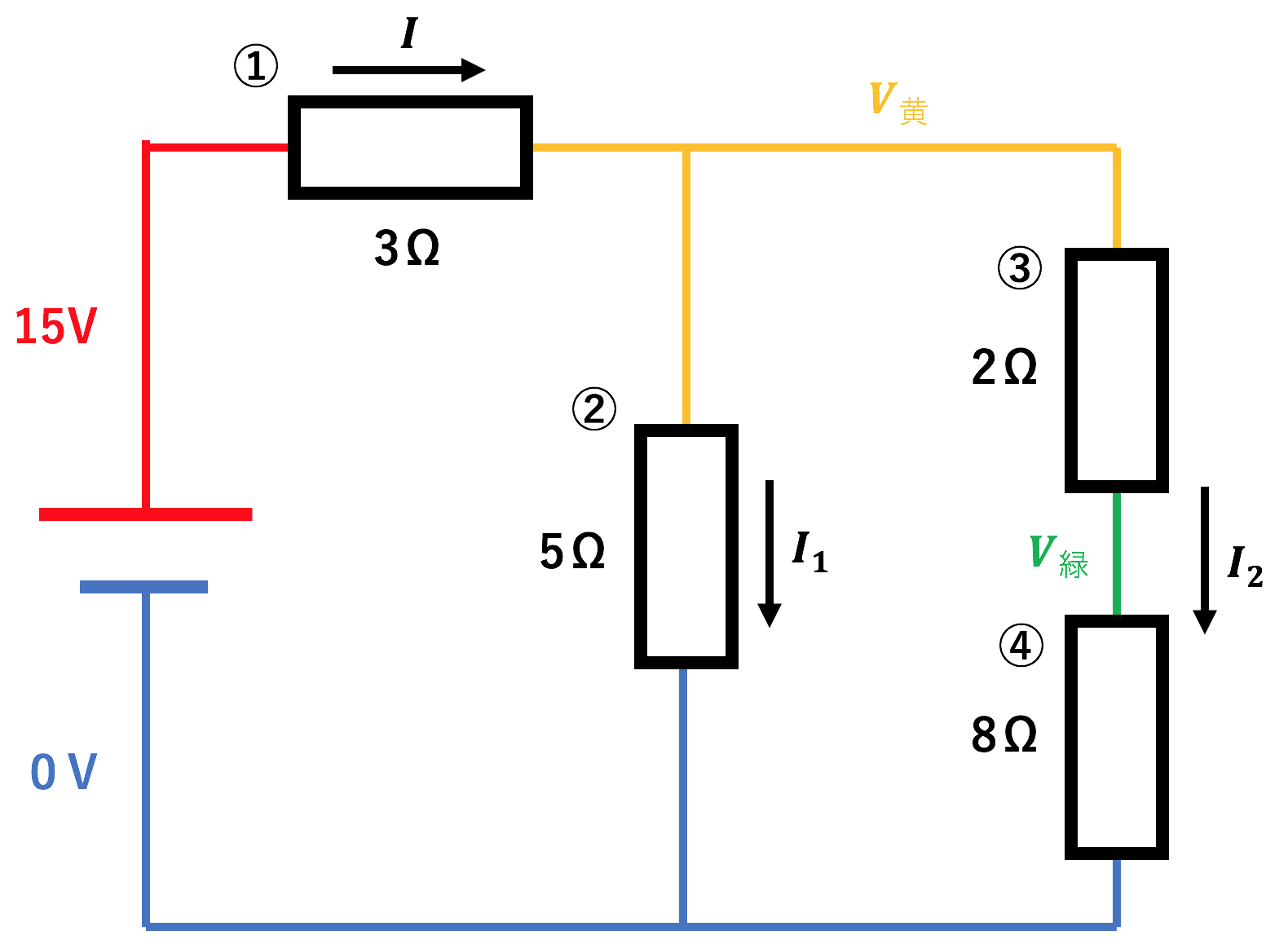
基本式:$V=RI$
①:$15-V$黄$=3×I$
②:$V$黄$-0=5×I$1
③:$V$黄$-V$緑$=2×I$2
④:$V$緑$-0=8×I$2
これに加えて、
$I$の電流は、$I$1と$I$2に別れているから、
⑤:$I=I$1$+I$2
この①〜⑤の式を計算すると、、
すべての場所の
電位も電流もわかる
ってのが、
高校の電気回路なんですわ。
おーけー?
基本式 $V=RI$は、個別で使うのです。
今回は、ぜんぶ抵抗だった例ですが。
コンデンサやコイルがあっても同じこと。
わからない値はぜんぶ文字で置いて、
個別で式を立てるのが高校レベル
これが、大学教授が求めている解き方。
高校生らしい、
入試に有効な解き方なんですな。
■わからない値は文字で置く
■各素子(抵抗、コンデンサ、コイル)で個別で式を立てる
以上!
こう解かないんだったら、
落ちてもしゃーないわなっw
あは


